Choosing a power supply for n + m redundant apps

Choosing a power supply for n + m redundant apps

Here are the criteria you need to successfully design a parallel ac/dc front-end power supply

BY ROY ALLEN
Power-One
Camarillo, CA
http://www.power-one.com

This article provides an overview of the concepts required to enable successful paralleling of ac/dc front-end power supplies. Although much of this discussion can be applied to applications that require a battery backup, such as 48-V telecom central-office equipment, ac/dc front ends do not typically include use of a battery backup and therefore do not include battery controllers and associated equipment.

Generally, the requirements for paralleling ac-input front ends (see Fig. 1 ) also apply to dc-input front ends; the only difference between these units once installed in the end system is the input source. Dc-input front ends allow equipment primarily designed to operate from utility-ac inputs to alternatively be operated from the 48-V battery-backed supplies commonly found in telecommunications applications.

Fig. 1. The backplane-mounted ac connector on the product on the left enables true hot-swap operation. The front-mounted ac receptacle on the product on the right ensures that ac is safely disconnected before the power supply is removed from the rack.

Paralleling basics

The three primarily reasons for paralleling power supplies are to increase total power, facilitate scalability, and provide redundancy.

Paralleling for increased power is done when the host-system power requirements cannot be met by a single power supply or if form-factor limitations preclude the use of one power supply. An example is when two 1U-high power supplies are used instead of a single 2U supply that would not fit within the height constraint of a 1U rack.

Although each power supply should equally power its portion of the load, there is always some degree of current-share imbalance. Therefore, supplies must either be designed for paralleling, or the power supplies must use external circuitry to accomplish the task.

Paralleling for scalability is done to provide power supplies that cover both small and large applications. This approach facilitates the addition of incremental power when the needs of an individual site increase, and reduces the number of power-supply model numbers in spares inventory when servicing multiple sites.

Paralleling for redundancy (see Fig. 2 ) is done because many mission-critical infrastructure systems require very high availability. Applications include medical life support, communications, and air-traffic control. Power systems used in these applications require redundant operation so that in the case of single or multiple power fault conditions, the mission-critical system can operate without interruption.

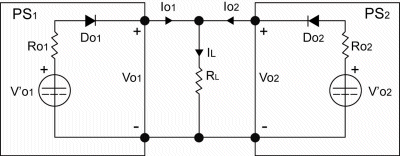
Fig. 2. Two power supplies are paralleled for redundant operation using ORing diodes DO1 and DO2 . Although not shown explicitly, this circuit would generally require a current-sharing methodology to operate reliably.

Redundancy is generally accomplished by paralleling two or more supplies to ensure that adequate power is available in the event of a power supply failure. Each power supply uses ORing circuits to isolate the outputs; enabling functioning supplies to work together and effectively disconnecting any defective supply’s output from the paralleled bus. This effectively protects the power bus, increasing the availability of the host system.

Calculating availability

Redundant power systems can be implemented in many ways, each having an impact on the availability of the system. Consider the following system designs:

• Two redundant supplies in parallel. If one fails, the other must assume the full system load requirements. Each supply must be sized to handle the entire system load. Three redundant supplies in parallel. If one fails the remaining two supplies must be sized so that jointly they handle the system load.* Four power supplies with each supply capable of supplying 33% of the system requirement; only one supply could fail without affecting system functionality. Four power supplies with each supply capable of carrying 50% of the system load; up to two supplies could fail without affecting system functionality.

N + m paralleling

The nomenclature used to describe the redundant system in the above examples is called “n + m paralleling,” where for a redundant power system:

* n is the number of paralleled power supplies of some power level PSUP , required to operate a system without redundancy.* m is the number of redundant power supplies (spares) of power level PSUP , specified to improve the system availability.

If n+m supplies are used to power a system, n are needed to carry the load, and the availability of the power system increases exponentially as m increases.

• Typically, n is the number of supplies with output power PSUP , required to power the smallest system, PSYS , or n= (PSYS /PSUP ), rounded up to the next higher integer number. m is the number of spare supplies with output power PSUP , determined by the designer as necessary to provide the requisite level of system availability.

A typical method of determining the output power, PSUP , of each power supply is make PSUP = PSYS-MIN , where PSYS-MIN is the power required to power the smallest host system. Adding another supply to this would create a 1+1 redundant system for this provisioning level.

For larger systems, additional power supplies, or power PSUP , are added (n is increased). For instance, the next level of provisioning may require one additional supply to power the system. In this case, the system would operate from a n + m = 2 + 1 redundant power system. Systems requiring higher power would increase the n count.

Further improvement in availability may also include increasing the number of spares (m) used in the system. Most large systems require m=1 as a minimum, but very high availability systems may specify m = 2. However, not many systems today specify m > 2, because power supply MTBF has significantly improved over the last few years, and because of cost.

System availability is very dependent on the mean time to repair (MTTR) value of a system. Power supplies designed for use in high-availability environments have monitoring and signaling capabilities that allow external supervisory systems to monitor the operation of each supply and report failures. Failure reporting via dedicated signal lines or protocols such as I2 C, allows technicians to quickly locate and replace a failed unit; this functionality minimizes the MTTR, and increases system availability and MTBF.

Availability, A, of a system is the probability that the system is available. Since a system is either available or failed it follows that A + F = 1, where A is probability of system availability and F is probability of system in a failed state.

Therefore, system availability can be expressed as A = (1 F)

Further, the availability can also be expressed as:

APWR-SYS =MTBFSUP /(MTBFSUP +MTTRSUP )

where

APWR-SYS = Power system availabilityMTBFSUP = Mean time before failure of a single supplyMTTRSUP = Mean time to repair a single supply

MTBF data for a given supply is typically supplied by the power-supply datasheet and is a function of temperature. In the following analysis, make sure the MTBF values used are consistent with the operating temperature required. Individual supply MTTR data depends on the supply design and ease of repair; system MTTR is dependent on the end user’s ability to find and repair a failed supply within the system.

For example, if a power system uses only one power supply, with a rated MTBF of 25,000 hours at the required temperature, and has an MTTRSUP of 4 hours, then the calculated availability of the power system using one supply is 99.992% expected uptime. This 0.0080% power-supply downtime equals an average of 3.5 min/month.

For telecom and datacom systems, minimum availability is generally accepted to be at least 99.999%, a downtime of no more than 0.44 min/month. Continuous operating processors require even higher availability, which can easily translate into seconds/month downtimes. Depending on system-availability requirements, downtime cost/minute can vary from $100 to $100,000 or even higher.

If the above system were fitted with a second supply, the availability of the system would be calculated as:

A = 1-[(1-a)*(1-a)] = 1-(1-a)2

where

* A = System availability

* a = Availability of each supply

For the above example:

A = 1-(1-.99992)2 = 1-(0.00008)2 = 99.99999936%.

This translates to an average downtime of 0.00028 min/month, or ~ 17 ms! The addition of just one redundant supply to this system decreased the average downtime by a factor of ~200, and increased the effective power system MTBF to more than 312 Mhrs, providing an increase of over 6,000 times that of a single supply. Note that these multiplicative factors are strongly dependent upon the MTBF value of the single supply used. ■

For more on redundant power supplies, visit http://electronicproducts-com-develop.go-vip.net/power.asp.