Frequency response: A scope’s key, unseen, spec

Frequency response: A scope’s key, unseen, spec

The response shape of a digital oscilloscope is a key factorin its ability to reduce errors in amplitude and rise time

BY MIKE SCHNECKER
Business Development Manager
Rohde & Schwarz
www.usa.rohde-schwarz.com

Specifications for digital oscilloscopes typically include dc accuracy, 3-dB bandwidth, rise time, and overshoot but not the instrument’s frequency response. It’s not a surprising omission, as a Gaussian response was assumed throughout most of this venerable instrument’s history when all scopes and the signals they measured were analog.

But when scope architecture and signals became mostly digital, the scope could have one of many response types, from maximally-flat to Chebyshev, Butterworth, and Gaussian, but it remains unstated. Nevertheless, frequency response is an important scope characteristic, as it has direct impact on overshoot and ringing that contribute to errors in amplitude and rise time. Consequently, it is important to understand scope response and how it affects measurement accuracy.

Signal fundamentals

Any signal consists of the sum of sine waves at different frequencies and phases, and in the frequency domain they appear as spectral lines, each one weighted separately by the frequency response of the scope. Ideally, it is important to know how the frequency response weights each one of those components, but with only 3-dB bandwidth and rise time specified on the data sheet, the user has only a hint of what the frequency response might be.

The square wave is one of the most complex waveforms, as it contains frequency components ranging from very low to very high, and they occur simultaneously. The step response of the scope can be used to predict transient behavior, as Fourier theory dictates that the frequency response of an ideal step is a sin(f)/f function in the frequency domain. As this function contains an infinite number of harmonics (theoretically with an infinite bandwidth), it cannot be practically generated or measured.

Given this immutable limitation, the solution to building a scope that can measure a voltage step even though it has a limited bandwidth lies in low-pass filter theory. A low-pass filter is defined by its impulse response, and its step response is measured by convolving an ideal step with the impulse response. The impulse response is determined by the characteristics desired in the frequency and time domains.

Extremely high levels of rejection, although the Holy Grail in the RF filter domain, are unacceptable in a scope as the impulse response of the instrument would have to be infinite, an obvious impossibility. In addition, as a scope measures the rise time and amplitude of a rapidly-changing signal, a brick wall response is far from ideal, as its time-domain response has massive ringing. A flat response with very sharp roll-off can also be achieved only by accepting ripple (ringing) in the step response, while a more gradual roll-off in the frequency domain results in a slower step response and far less ringing. Based on the step responses for Chebyshev, Butterworth, and Gaussian filters (see Fig. 1 ), it is reasonable to assume that the Gaussian response is the best choice for a scope design.

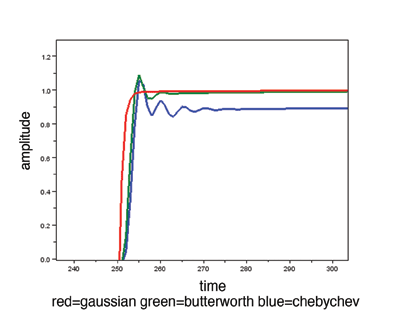
Fig. 1: Note that in the step responses of Gaussian, Butterworth, and Chebyshev filters shown, the Chebyshev and Butterworth responses show significant ringing while the Gaussian filter has virtually none.

Response philosophies

The “ideal” frequency response curve of an oscilloscope varies between manufacturers. Some believe that a maximally flat response provides the best results, as this response type does not deviate all the way to the instrument’s cutoff frequency after which it drops off precipitously. It also allows the instrument’s frequency range to be extended, resulting in very sharp rolloff characteristics.

The maximally-flat frequency response requires significant tradeoffs to be made in order to achieve it. For example, a penalty is paid at the transition frequency as there is no way the response can be perfectly flat and also transition without a “bump” occurring in the response at higher frequencies. Butterworth, Chebyshev, and other types of responses also produce some irregularity in the passband, even with current state-of-the-art of digital filters.

Scope manufacturers such as Rohde & Schwarz believe that the traditional Gaussian response represents the best trade-off between conflicting specifications and provides the best overall accuracy and the least ringing and overshoot. It has the unique ability to have a Gaussian response in both the frequency and time domains and does not ring in either one. The frequency response of the R&S RTO 1024 2-GHz scope along with a maximally-flat response of a 4-GHz scope (see Fig. 2 ) shows that the R&S RTO1024 response is nearly a “textbook” Gaussian shape. Comparing the step response of both scopes (see Fig. 3 ), the overshoot of the RTO1024 is just 1%, while the maximally-flat scope exhibits 8% overshoot.

Fig. 2: The Gaussian frequency response curve of the R&S RTO1024 (blue) and that of maximally-flat scope (green) superimposed on an ideal Gaussian response (violet) show how close the latter comes to an ideal response.

Fig. 3: The step responses of the two scopes show that the R&S RTO1024 (right) has about 1% overshoot, while it’s maximally flat counterpart (left) exhibits 8%.

Adopting the Gaussian response for scopes requires a trade-off narrower 3-dB bandwidth as the response rolls off gradually. However, this was deemed acceptable as it allows the highest accuracy to be achieved, especially at signal edges, the absence of ringing, and overshoot of less than 1%, far lower than the industry average of 5 to 10% or more. While both ringing and overshoot are key scope metrics, reducing overshoot (the maximum amplitude excursion expressed as a percent of the final amplitude) is extremely important, as it otherwise obscures the characteristics of the device under test, making accurate amplitude measurements impossible.

Obviously, frequency response is but one of many characteristics that determine the performance of a modern oscilloscope. Its ease-of-use features and many other characteristics are equally important to the decision. However, frequency response is nevertheless a major contributor to this performance of the instrument that largely goes unseen as it is not typically specified by the manufacturer. But it is important to know how it affects the measurement and provides insight into how the chosen scope performs. ■