Supercomputer cracks the world’s largest math problem, resulting in a 200 terabyte proof

Mathematical proofs of a certain scale ascend beyond the domain of human cognitive ability, requiring the aid of computer-driven calculation to articulate fully. One such problem, called the Boolean Pythagorean triples, eluded mathematicians for decades. But after simultaneously running 800 computer processors for two days, three computer scientists have finally solved the poof—all it took was 200 terabytes worth of data, the digitized equivalent of all the text held by the US Library of Congress.

The practice of using computers to solve mathematics is a staple of combinatorics—the branch of mathematics dealing with combinations of objects belonging to a finite set of discrete structures—and involves scouring through vast pools of information until an exception to a rule is discovered. Until now, the record holder for the largest proof was held by a 13-gigabyte file, published in 2014.

By contrast, the Boolean Pythagorean triples proof required 15,000-times more data.

Initially proposed in the 1980’s by University of California mathematician Ronald Graham, the proof asks whether it is possible to color each positive integer red or blue so that no trio of integers which solve the Pythagorean theorem a ²  + b ²  = c ² can all be the same color. At the time of its conception, Graham offered a $100 reward to any mathematician who could solve it. 36-years later; Graham finally presented the check to three researchers: Marjin Heule of the University of Texas at Austin, Oliver Kullmann of Swansea University, UK, and Victor Market of the University of Kentucky in Lexington.

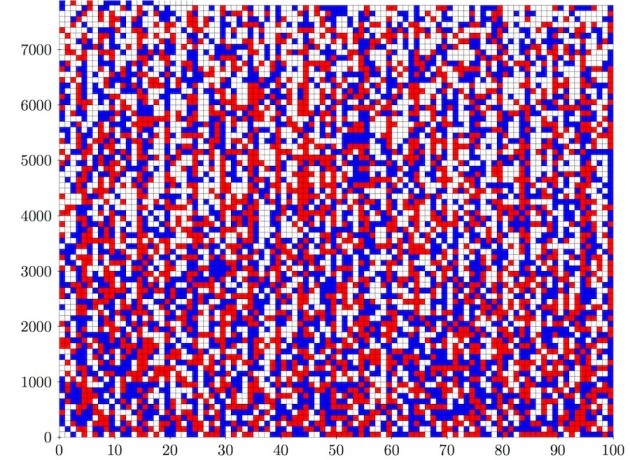
In a paper posted on the arXiv server , the three scientists have demonstrated that there are more than 10^2,300 ways to color integers all the way up to 7,824, but after 7,824, it becomes impossible for every Pythagorean triple to be multicolored because the number of verifiable variables skyrockets into the trillions. But by applying several techniques from number theory, the researchers knocked off all obvious impossibilities, dropping the total number of variables to just below one trillion. Even under these circumstances, processing this much data required running the University of Texas’ Stampede supercomputer for 48 consecutive hours. Once the computer’s 800 cores finished scrubbing through all the possibilities, the researchers used standard software to verify the proof.

Having successfully cracked the Boolean Pythagorean triples puzzle, Kullman and his team continue to remain baffled as to why the coloring is impossible, or whether the number 7,825 holds any significance. Such a predicament is not unheard off, echoing a common objection over the mathematical value of computer-assisted proofs.  Many argue that the mathematician’s goal is to increase our understanding of mathematics by discovering theories to make sense of solutions, not to simply amass an ever increasing pool of facts dependent on ticking off possibilities through computer processing.

Source: Nature