Enhanced MCUs enable fast real-time control systems

BY KENNETH W. SCHACHTER
C2000 Technical Staff, Texas Instruments
www.ti.com  

Engineers designing real-time control systems are constantly faced with the challenge of optimizing performance. These systems require minimal latency, where the time delay between sampling, processing, and outputting must fit within a tight time window to meet the control loop performance specifications. At the heart of the control systems are math-intensive algorithms, which are used to calculate the control signals. Using a microcontroller (MCU) that can quickly and efficiently execute mathematical operations is critical toward system timing constraints. Ideally, this MCU would be able to execute the real-time control loops concurrently with the central processing unit (CPU). For example, some systems may need to support power line communications using the same MCU. This article will highlight various enhancements that can be implemented on an MCU to accelerate its performance.  

High-performance MCUs for real-time control systems depend on having an extremely fast CPU. This CPU usually includes hardware support for fixed-point and floating-point mathematical operations. Many control system designs start with simulation tools, where the algorithms are developed with floating-point math. These algorithms can then easily be ported to an MCU that has native floating-point math support. Floating-point math provides a large dynamic range, thereby making it easier to develop code than using fixed-point. The programmer no longer needs to worry about scaling and saturation. Additionally, robustness is improved because floating-point values do not wrap around the number line on an overflow or underflow, as they would in fixed-point math. Along with mathematical operations, the MCU architecture should be optimized to support high-level language programming (especially C) and have seamless support from a complete set of development tools.  

Trigonometric and arithmetic operations commonly used in real-time control algorithms include Park and inverse Park transforms, space vector generation, direct-quadrature-zero and inverse direct-quadrature-zero transforms, FFT magnitude, and phase calculations. Typical math operations include sine, cosine, arctangent, divide, and square root. These types of operations are very cycle-intensive and they can greatly affect the overall system performance. By augmenting the floating-point capabilities of the MCU with an extended instruction set, these operations can be much more efficient. To accomplish this, the compiler needs to have support for automatic generation of the trigonometric and arithmetic instructions. The compiler can then use these instructions, where applicable, instead of run-time support library calls, resulting in significantly fewer cycles and dramatically increased performance. Also, portability will be maintained because the same code can be used on an MCU with and without this enhanced math support.

Achieving the ultimate level of high performance for computation and efficient processing, which is critical for designing many of today’s complex real-time control applications, might require the need for an independent co-processor specifically designed for control law acceleration. For example, a typical power digital controller consists of an input A/D converter, a math engine to compute the control law algorithms (e.g., PID, two-pole/two-zero, and three-pole/three-zero compensators), and a PWM channel to output the calculated waveform. Many advanced control systems would greatly benefit from an architecture that integrates these functions in hardware to minimize latency, yielding the absolute minimum sample to output delay. This architecture would execute time-critical control loops concurrently with the main CPU and free it up to perform other required tasks. In addition, the architecture would have a built-in protection mechanism to guard against over-current and over-voltage conditions.

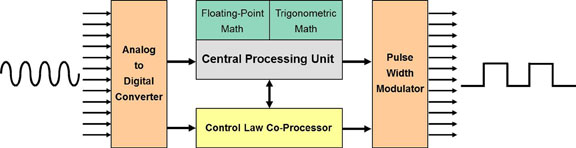
Fig. 1: An enhanced real-time control system block diagram.

The system’s independent hardware accelerator must be optimized for 32-bit floating-point math-intensive computations. This accelerator is perfect for managing low-level control loops, with high-performance improvements over using the CPU. Additionally, it needs to directly access memory and have direct access to various control peripherals, such as the A/D and PWM modules, to minimize latency. Ideally, it needs to be able to read the A/D results immediately after conversion is completed to reduce delay and enable fast system response.  

Designing this accelerator such that it responds to peripheral triggers without CPU intervention is very efficient since it does not use interrupts for hardware synchronization, nor must it do any context switching. This approach eliminates jitter and the execution time becomes deterministic. For flexibility, this accelerator should be fully software-programmable rather than fixed hardware-based. The independent accelerator can be set to a low-power mode when not executing the control law, potentially offering significantly more power-efficient operation compared to the main CPU. The advantages provided by this independent co-processor accelerator can significantly enhance real-time control applications, such as motor control, power conversion, renewable energy, and electric vehicles.  

Adding functionality for intelligent management and communications to advance control systems can optimize efficient operation. Using power line communications is ideal for intelligent management since the existing infrastructure can be used cost-effectively. To solve performance issues and avoid the complexity and cost of adding another processor, the MCU can be enhanced with a tightly coupled fixed-point accelerator that greatly improves the performance of power-line communication connections. This accelerator adds an extended set of registers and instructions to the MCU and needs to be capable of supporting various communication technologies. The four key operations that consume most of the processing power are Viterbi decoding, complex FFT, complex filters, and cyclical redundancy check (CRC).  

Besides communications, this accelerator would be very useful for general-purpose signal processing applications, such as filtering and spectral analysis. For example, spectral analysis can be used to process motor-vibration noise to determine the health of a system and estimate the motor’s operating life. A complete library of functions is also available, making the programming much easier and more efficient.

One example of a real-time enhanced MCU would be the 32-bit C2000 from Texas Instruments that features four accelerators: a floating-point unit, a real-time control co-processor, a trigonometric math unit, and a Viterbi, complex math, and CRC unit. You can find out more by reading the white paper, “Accelerators: Enhancing the Capabilities of the C2000 MCU Family,” which can be found under “Technical documents” at: http://bit.ly/2aVBak5 .