High-speed A/D converter real-time calibration

BY DJAMEL HADDADI
Technical Lead
Integrated Device Technology
www.idt.com

The explosion of mobile data is driving new receiver architectures in communication infrastructure that can provide higher capacity and more flexibility. These next-generation circuits are software defined radio systems based on power-efficient RF A/D converters that are capable of sampling directly at the antenna and delivering high dynamic range. Such A/Ds are designed in very advanced CMOS technologies using time-interleaved (TIADC) architecture to achieve very high sampling rates. This architecture suffers from time-varying mismatch errors that necessitate real-time calibration. We describe in this article a novel background calibration method for gain and timing mismatch errors through low complexity digital signal processing algorithms.

Mismatch errors in two-channel TIADC

An efficient way to double the speed of an A/D is to operate two in parallel with out of phase sampling clocks. The unavoidable small mismatches between the transfer functions of the sub-A/Ds result in spurious tones that degrade significantly the achievable dynamic range. There are four types of primary errors:

1. Dc offset error
2. Static gain error
3. Timing error
4. Bandwidth error

The dc offset error is very simple to handle in practice through digital calibration. The bandwidth error is the most difficult to deal with and it is usually mitigated through careful design and layout. We will focus in this article on gain and timing errors calibration as they are the major contributors to dynamic range loss.

A calibration method

In practice the Nyquist bandwidth of an A/D is never fully used, and a fraction of it is usually dedicated to the roll-off of the anti-aliasing filter. This free band can be exploited to inject a constrained calibration signal. A sine-wave is selected for calibration as it is easy to generate with high spectral purity on which we impose two main constraints:

1. The amplitude is kept small enough to avoid any impact on dynamic range, while providing enough estimation accuracy. Experiments show that -40 dBFS to -35 dBFS level range provides the best tradeoff for a 14 bit A/D.
2. The frequency is limited to the following discrete values in order to reduce the complexity of the digital signal processing algorithms:

Where F_s is the TIA/D sampling frequency, P, K are unsigned integers and S=+-1 depending on the location of the calibration signal with relation to the edge of the Nyquist zone (see Fig. 1 ). This signal can be easily generated on-chip with a fractional-N PLL using the clock of the A/D as a reference signal. By choosing K high enough, the harmonics of the calibration signal will alias outside the useful band which relaxes their filtering requirements. The gain swing adjustment can be achieved with a programmable attenuator placed at the output of the PLL.

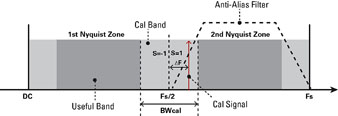
Fig. 1:  Frequency plan showing the location of the calibration signal.

If x0 and x1 denote the outputs of the two sub-A/Ds with the calibration signal as input, it can be shown using Eq. 1 that these two signals are linked by the following expression (the noise being ignored):

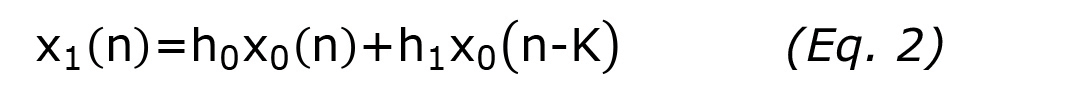
The coefficients h₀ and h₁ of this linear filtering formula are related explicitly to the gain g and timing ∆t errors by:

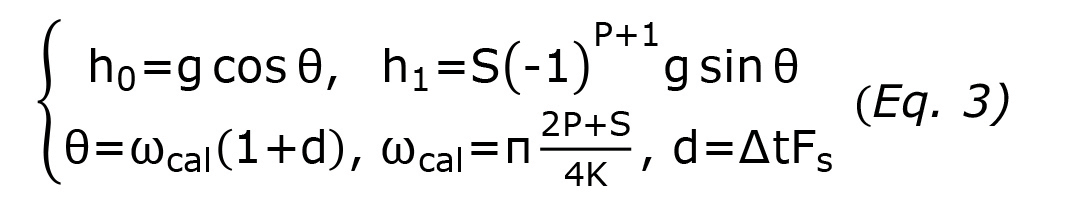
This nonlinear set of equations can be linearized and inverted by using a first order approximation, given the fact that the mismatch errors are kept small by design.

The estimation algorithm consists of three steps:

1. The calibration signal is extracted and cancelled from the output of the sub-A/Ds using an LMS algorithm, yielding the discrete-time signals x0 and x1. This algorithm requires a digital cosine/sine reference signals at the calibration frequency. The cosine signal is generated with a small look up table of size 4K (K
2. The coefficients h0 and h1 are estimated, adaptively, from the extracted x0 and x1 signals using an LMS algorithm as shown in Fig. 2.
3. The gain and timing errors are then computed from the linearized set of equations as derived from Eq. 3.

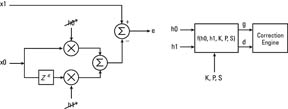
Fig. 2:  Background estimation of gain and timing errors through a 2-tap digital adaptive filter.

Once estimated, the gain and timing errors are used to feed a digital correction engine. The gain is compensated using a simple digital multiplier. The correction of the timing error is accomplished with a modified fractional delay filter_. Polyphase and symmetry are exploited to reduce the implementation complexity of the filter. Both the estimation and correction engines operate at the sub-A/D sampling rate. Down-sampling can be envisioned for the estimation block for further optimization.

Proof of concept

A composite test signal consisting of a TM3.1, 20 MHz LTE carrier centered at 300 MHz, and a 253.44 MHz, -35 dBFS calibration sine-wave, corresponding to S=1, K=8, P=2K, was generated using the test setup shown in Fig. 3. This provides very high dynamic range thanks to low noise and high linearity D/A converter and DVGA. We have used a commercially available 14 bit/500 Ms/s TIA/D that integrates high resolution tunable gain and timing errors. The A/D raw data was captured with an FPGA and processed with our calibration algorithm using Matlab software. The gain and timing errors of the TIA/D have been set to about 0.5 dB and 5 ps, respectively, to simulate a worst case situation.

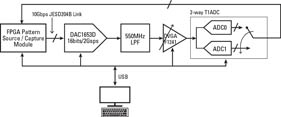
Fig. 3:  Block diagram of the test setup.
Figure 4 shows the power spectrums of the data before and after calibration. The LTE carrier image, at -80dBFS before calibration, has been reduced by about 30dB to -110dBFS level after calibration. The calibration signal and its image have been completely cancelled by the extraction and cancellation algorithm. This performance has been achieved within about 200us convergence time.

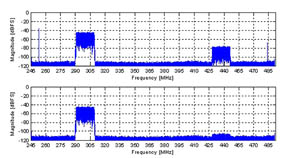
Fig. 4: Power spectrums before (TOP) and after calibration (Bottom) with 300 MHz LTE carrier.

The calibration signal was kept unchanged and the LTE carrier center frequency has been swept from 50 to 400 MHz in order to assess the frequency behavior. The resulting image rejection (see Fig. 5) shows that at least 30 dB dynamic range improvement is maintained across the two first Nyquist zones. As expected, the image rejection decreases with frequency – limited by the contribution of the bandwidth error which is not corrected.

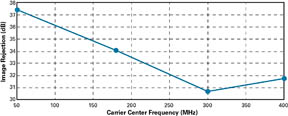
Fig. 5:  Image rejection versus the LTE carrier center frequency with fixed calibration signal.