Protecting inverters using thermistors

Inverters are electrical systems that provide variable voltage (ac output) when connected to a dc-input source. Inverters are available in two varieties: three phase and single phase. These inverters are also known as static frequency chargers or variable frequency drives. The devices are available in two varieties: three-phase and single-phase. As most inverters are designed with a minimum amount of resistance to increase their efficiency and minimize losses due to heat, a common cause for failure in the devices is overloading by the inrush current. This case study provides an example of an overload scenario and demonstrate how it can be addressed using a thermistor. In addition, examples of simple NTC thermistors in inverter circuits are provided. In these circuits, the thermistors minimize the effect of inrush current on components, such as bridge or link capacitors.

Issue
Inverters experience failure due to inrush current pulses from the grid causing stress on components, such as filter capacitors, which are used as filters to reduce ripple effect. Table 1 shows the components of an inverter and the reasons for component stress:

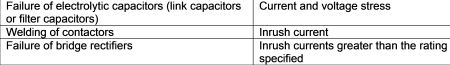
Table 1: Components of an inverter and the stress they get

Another common failure of inverters due to inrush current is overloading the inverter. This is due to the fact that most inverters are designed with a minimum amount of resistance in order to increase their efficiency and minimize losses due to heat.
For example, an overload condition will occur if you switch on three appliances — one by one — connected to an inverter. Consider the following:
• A 1,000-W inverter (more specifically, a 1,500-W inverter with 50% total overload capacity)
• Three standard appliances: a 300-W refrigerator, a 300-W LCD television, and a 300-W computer. The total load for these appliances is 900 W
• A 1,000-W inverter is capable of running these three appliances

An overload condition happens because of the energy required for startup. This inrush current can produce up to 900 W, or 3 times the rated power, for each appliance.
The inverter overloads in the following scenario:
• Step 1: If we switch on the first appliance, the load is 900 W, which is less than the rated capacity of the inverter. Thus, no overload situation is encountered.
• Step 2: If you switch on the second appliance, the total wattage needed is as follows:
First appliance (300 W) + second appliance (900 W) = 1,200 W. No overload situation is encountered.
• Step 3: If you switch on the third appliance, the total wattage needed is as follows:
First appliance (300 W) + second appliance (300 W) + third appliance (900 W) = 1,500 W.

An overload condition is encountered as soon as the third appliance is switched on to the inverter output (see Fig. 1a ).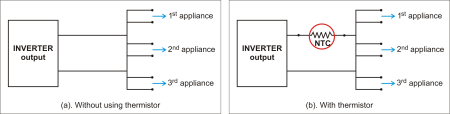 

  (a)                                                                            (b)

Fig. 1: The overload of an inverter (1a) can be controlled with a thermistor.

Solution
A thermistor (see Fig. 1b ) can be used to address the overload scenario of the sample problem. As per Step 3 above, the inverter wattage needed, including the overload condition, is >1,500 W. The maximum output power allowed is 1,000 W, while the allowed current is 8.0 A (1,000 W/120 V). The normal continuous current per appliance is 2.50 A (300 W / 120 V), and 7.50 A due to inrush current (2.50 A x 3). The duration of the inrush is 0.02 s (one cycle = 1 x 1/50 s). The energy the thermistor needs to handle without self destruction is 18.0 J (120 V x 7.50 A for 0.02 s). So, for three appliances that start up at the same time, 54 J is needed (3 x 18.0 J). A minimum resistance of 21.21 Ω (peak voltage/maximum allowable current: 120 V x 1.414/8.0 A) ensures that the current does not exceed 8.0 A. So if we assume an ambient temperature of 50°C and minimum resistance of 40 Ω, we can reconnect.
There are two methods for solving this situation.

Method A  
In the circuit in Fig. 2 , a 50-Ω, 4.0-A, 75-J NTC (UL recognized (E209153) and CSA recognized (CA110861) is used to bypass the surge after one second.

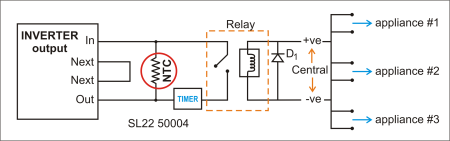
 Fig. 2: Method A for successfully starting up three appliances at the same time

Note that the NTC does not interfere with the efficiency of the inverter, since the relay is also protected from the inrush current by the thermistor. The thermistor will conduct through the relay with 99.2% efficiency.

Method B

In Fig. 3 , two 40-Ω, 10-A, 500-J NTCs are used.

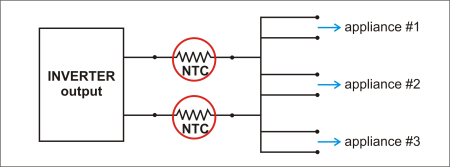
 Fig. 3: Method B for successfully starting up three appliances at the same time

• Efficiency = Δ Power / Input power
• Δ Power = Input power – losses due to thermistor
• Losses due to thermistor = I2(hot resistance)
• Where hot resistance = 0.22 Ω
• Losses due to thermistor = (8 A)^2 (0.22 Ω) = 14.1 W
• Efficiency = 985.90 W / 1,000 W = 98.6%
• Conclusion: Method B is more cost effective 

Selecting thermistors for inverter circuits
Simple NTC thermistor applications are shown in the three circuits (see Figs. 4, 5, and 6 ) below. These thermistors minimize the effect of inrush current on components, such as bridge or link capacitors.
The application shown in Fig. 4 involves an inverter powered by 12-V, 40-A battery input and 120-V 4-A output. 
 

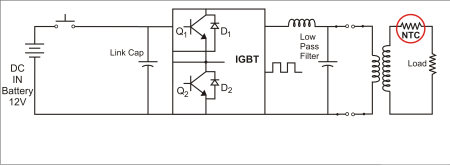
 Fig. 4: Classic inverter circuit.

The peak inrush current as measured on the oscilloscope is 400 A, due to the low impedance of the inverter. The frequency is 50 Hz. The following values can be calculated:
Inductive reactance (XL) = input voltage / inrush current:
XL=12 V / 400 A = 0.03 Ω

Inductive reactance (XL) also = 2 πfL, where f = frequency and L = inductance:
0.03 Ω = 2*(3.14)*50 Hz*L
L= 95.5 µH

Energy (E) the thermistor needs to handle without self-destruction = ½ LI2, where L = inductance and I = peak inrush current:
E= ½ (95.5*10-6)(400 A)2=7.64 J

Steady state current rating = I:
P_out of transformer = P_in of transformer
120 V*I = 12 V*40 A, I = 4 A

Minimum resistance required = V_peak / max tolerable inrush current (assume max tolerable inrush current =1/4th of the maximum measured):
400 A*¼ = 100 A max

Minimum resistance = 12 V / 100 A = 0.12 Ω

Since thermistors are temperature dependent, care must be taken to select the correct part. Assume the ambient temperature is 50°C. For most NTCs, resistance at 50°C is ½ the resistance at 25°C. So the correct minimum resistance for this application would be 0.24 Ω (2*0.12 Ω). For safety purposes, select a thermistor with a higher steady-state current rating than 4 A and double the energy rating.

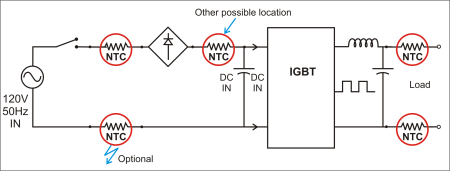
Fig. 5: Example of a typical frequency charger circuit.

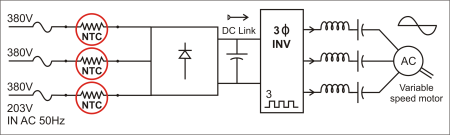
Fig. 6: Example of a typical variable frequency driver that minimize the effect of inrush current on link capacitors.

For more information see http://www.ametherm.com/