Sampling rate’s impact on oscilloscope bandwidth

Sampling rate’s impact on oscilloscope bandwidth

A digital scope’s effective bandwidth of isn’t determined merely by analog componentsthe digitizer and memory also play a role

BY PHIL STEARNS
Agilent Technologies
Santa Clara, CA
http://www.agilent.com

When selecting an oscilloscope for a specific measurement, the first thing that most of us consider is the bandwidth we’ll need to accurately reconstruct our signals. After all, the scope’s bandwidth tells us what spectral frequencies will be preserved and the maximum signal transition speeds that can be accommodated.

Oscilloscopes are designated by their nominal bandwidth, such as “the 500-MHz Model XYZ” and most even have the bandwidth specification embedded in their model number,

However, this “banner” specification only describes the maximum bandwidth allowed by the scope’s front-end circuitry. A scope’s effective bandwidththe maximum frequency components of a signal you’ll be able capture, store, and displayis determined by its sampling rate, which, in turn, can be constrained by the depth of its acquisition memory.

Briefly exploring the relationship among bandwidth, sampling rate, and memory depth can provide an understanding of the tradeoffs involved in selecting a scope and how to mitigate their effect so as to make measurements with more confidence.

A quick visit with Dr. Nyquist

The familiar Nyquist-Shannon sampling theorem states that a signal can be reconstructed exactly if:

the signal is band limited and the sampling frequency is greater than twice the signal bandwidth.

If we can assume that all samples are equally spaced in time, then any oscilloscope must maintain a sampling rate of twice its nominal bandwidth to avoid bandwidth degradation in the captured signal.

However, this theorem also assumes a theoretical filter, called a “brickwall” filter, that not only passes all frequency components below the bandwidth’s top frequency limit, but also eliminates all frequency components above this bandwidth (see Fig. 1 ). A high-performance oscilloscope with hardware/software brickwall filtering may be able to accommodate a sampling rate as low as 2.5 times bandwidth. But for mainstream oscilloscopes, such filters are generally impractical, and undesirable.

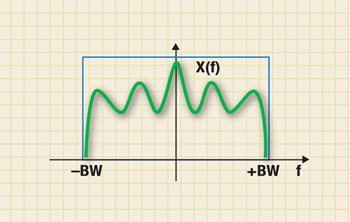
Fig. 1. With a perfect brickwall filter, sampling approaches the theoretical 2x-plus limit of the Nyquist-Shannon sampling theorem.

In a typical mainstream oscilloscope, the filter rolloff is not as aggressive (see Fig. 2 ). These filters can be implemented more economically, and their time-domain response is more predictable. The tradeoff is that you must employ a more conservative sampling rate, oversampling the bandwidth by a multiple of 4x.

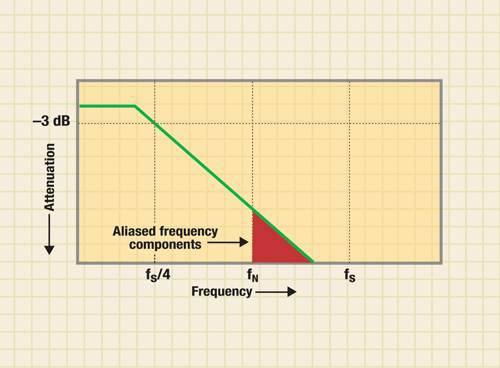
Fig. 2. Practical scope input filter characteristics dictate more conservative oversampling, typically by a factor of 4x.

As long as we maintain this 4x oversampling, the scope’s nominal bandwidth is maintained. However, anything that causes a reduction in sampling rate will lead to aliasing below the nominal bandwidth frequency.

Memory’s role

Memory and sampling rate are intertwined specifications. Because scopes have a fixed display window at any particular time-per-division (t/div) setting, there are few settings where both time and memory are maximized. However, it is more important to maintain the data acquisition (sampling) rateand therefore the bandwidth of the scopethan it is to use all the memory.

A simple calculation can tell you how many data points are required to fill your display: pts per waveform = sampling rate x t/div x number of divisions.

Consider, for example an oscilloscope with a 5-Gsample/s sampling rate and 10 time divisions set to 100 ns/div. Then the number of points per waveform is equal to 5 x 109 pts/s x 100 x 109 s/div x 10 div, or 500 points.

As long as the oscilloscope has enough memory to fill the display, the sampling rate can be sustained. However, if the sampling rate is so high it would result in data exceeding the maximum amount of memory, the sampling rate must be reduced to fill the allotted time.

How sampling rate is reduced with slower sweep speeds is easily grasped graphically (see Fig. 3 ). For two hypothetical 500-MHz-bandwidth oscilloscopes, the oscilloscope with more memory can sustain a high sampling rate over more settings. So why does that matter? Let us return to our Nyquist analysis.

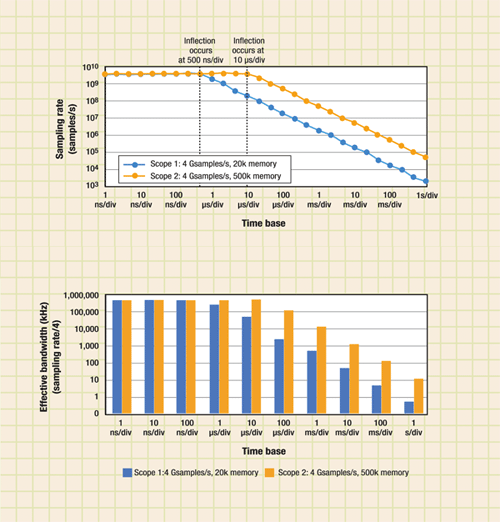
Fig. 3. Sampling rate must drop to fill memory with enough data for display (left). The drop in sampling rate limits the scope’s effective bandwidth (right).

Scope 1 will oversample the maximum bandwidth by a factor of 8 at all t/div settings above 500 ns/div (see Fig. 3a ), at which point the sampling rate begins to drop. However, it is not until the sampling rate drops below 2 Gsamples/s (4x oversampled) that aliasing becomes a concern. This occurs at 1 μs/div. At that point, any decrease in sampling rate causes the scope’s effective bandwidth to drop (see Fig. 3b ).

Implications

The above analysis leads us to three conclusions:

Bandwidth is constrained by the effective sampling rate of the oscilloscope.Sampling rate can be degraded at slower t/div (sweep) speeds.Increasing acquisition memory can delay the onset of sampling rate degradation.

How does this impact your scope selection and debugging methodology? Well, it really depends upon the signals you are viewing.

If you spend most of your time with simple signals like rising edges and transient events, it’s easy to match your scope’s timebase to the spectral content of your waveforms – fast edges require fast sweep speeds.

If you look at more complex signals that combine slow events and fast events (like modulated signals or trending signals), you should consider replacing a shallow memory oscilloscope (fewer than 100 ksamples) with a deeper memory model (at least 1 Msample).

If you cannot change your current equipment, you may want to break your analysis into manageable steps. Use slower t/div settings to characterize slower trends; then switch to faster settings to characterize high-bandwidth-signal events. If you choose this path, you may want to use the above calculations to plot the t/divbandwidth relationship of your scope.

For single-shot acquisitions, the tradeoff between bandwidth and effective sampling rate is identical, but the mental model and implications are slightly different. In a single-shot acquisition, you want to sample for as long as you can (as long as your measurement requires) as fast as you can. A high sampling rate is important for maintaining signal fidelity while zooming in on a signal trend for details about individual transitions. It allows accurate measurements of both macro- and micro-events in a one acquisition. If you can’t maintain a high sampling rate (bandwidth), these events should be measured with separate acquisitions.

A final word

While the information presented here should help in understanding important attributes of scope performance, bear in mind that it has been a somewhat cursory examination of the relationship between bandwidth, sampling rate, and memory. The subject of bandwidth is much more nuanced, with factors like passband flatness and frequency rolloff deserving much more attention than can be given in the scope of a brief article.

To explore this topic in greater depth, two application notes are of particular value: Evaluating Oscilloscope Sample Rates vs. Sampling Fidelity: How to Make the Most Accurate Digital Measurements ( AN-1587) and Choosing an Oscilloscope with the Right Bandwidth for Your Application (AN-1588). Both of these application notes can be found online at http://www.agilent.com using the site’s search function

Get more information on oscilloscopes at http://electronicproducts-com-develop.go-vip.net/testmeasure.asp ■