Wheatstone Bridge Calculator

Wheatstone bridge is a very useful circuit. When the resistors on the right side have exactly the same values as their counterparts on the left side (R1 = R3 and R2 = Rx), the bridge is said to be perfectly balanced, and the voltage V_B is zero. However, with a small change in resistance R_X, the bridge becomes unbalanced, resulting in a non-zero voltage for V_B. With a differential amplifier across V_B's terminals to extract the differential signal while rejecting common mode noise, very small changes can be detected precisely. Common applications for the Wheatestone bridge circuits include strain gauges, pressure gauges, and other sensors and measurement equipment.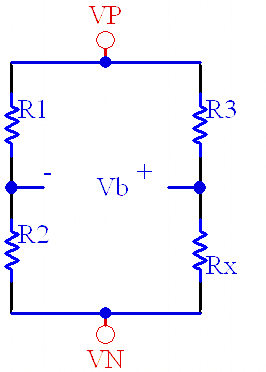

The bridge voltage is calculated as follows:

V _B = V _in * [Rx / (R3 + Rx) - R2 / (R1 + R2)]

If R3 = R1, and Rx = R2 + delta, then:

V _B = V _in * (R2 + delta) / (R1 + R2 + delta)-R2 / (R1 + R2)]

Now, if we assume that delta is smaller than R1 + R2

V- = ~ V _in * [delta / (R1 + R2)]

Therefore, we can see that the bridge voltage is approximately proportional to the error delta divided by the sum of resistance on one side.

Given the bridge voltage, we can calculate the unknown resistor value.

(R1 + R2) * (R3 + Rx) * V _B / V _in = Rx * (R1 + R2) + R2 * (R3 + Rx)

Rx * (R1 + R2) + R3 * (R1 + R2) * V _B / V _in V _B / V _in = Rx * R1 + Rx * R2, - R2 * R3-Rx * R2,

Rx * R1 - Rx * (R1 + R2)   R2 * R3 + R3 * (R1 + R2) * V_B / V _in = V _B / V _in

Rx = (R2 * R3 + R3 * (R1 + R2) V _B / V _in ) / (R1-(R1 + R2) * V _B / V _in )